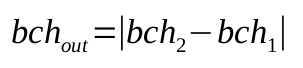This post walks through the math and architectural decisions behind the token-liquidity app used by the Permissionless Software Foundation. The app is an automated market-maker that allows for permissionless trading between a token and Bitcoin Cash. Send it tokens, it sends you BCH. Send it BCH, it sends you tokens. That's the basic idea behind how it works.
The mathematics built into the app represent an attempt to create a community-based pseudo-stable token for rewarding and incentivizing developers that contribute to the Foundation's open source software projects, but the app could be adjusted to fit any community currency.
Overview
The token-liquidity app is a JavaScript application written in node.js which is inspired by the Bancor whitepaper and the ideas of creating community-based currency as explored in this video. It's an automated, permissionless market-maker which allows a community token to achieve perfect liquidity between itself and Bitcoin Cash.
The mathematics behind the smart-contract described in Bancor's whitepaper were manipulated and adjusted to create a similar but new type of automated market-maker. The app constantly adjusts its exchange rate in order to provide 'guard rails' against market panics and irrational exuberance. The price of the token is still subject to free-market supply-and-demand, but it is strongly encouraged to fluctuate within a psudo-stable range of prices.
In this way, the app makes it easy for the community to manage the value and stability of their token.
The Base Equation
The basic equation controlling the exchange rate of the application is based on the natural logarithm:



The basic equation above governs the balance of the token-liquidity app. The app will constantly adjust its exchange rate in order to maintain a balance of tokens and BCH governed by the equation above. This equation has several advantageous properties:
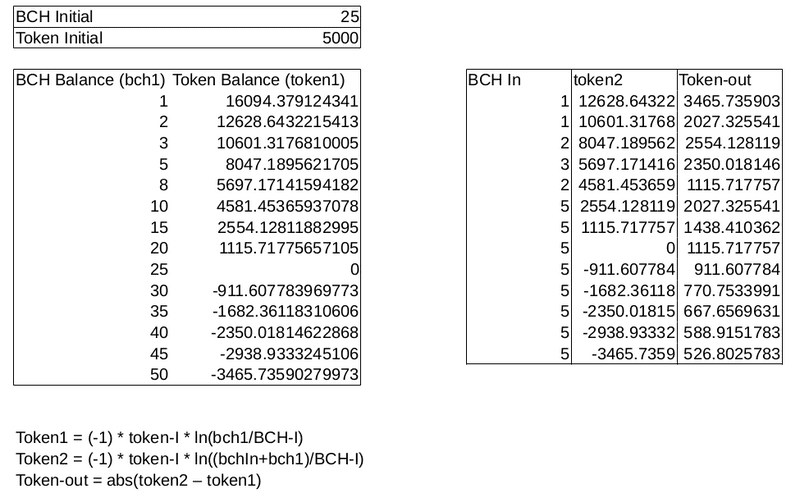
- The BCH never goes to zero. As more tokens are added to the app, the exchange rate is adjusted so that the total amount of BCH can never be extracted. The app can never run out of BCH.
- There is a psudo-stable range to which the app will naturally gravitate. This is expressed in the -5000 to 5000 range in the graph above, but this range is adjustable by setting the initial values of the equation.
- It's easy to control the exponential price increase by creating new tokens and sending them to the app. This lowers the price, bringing it back to the psudo-stable range, and allows the community to capture BCH for funding projects.
- When the BCH balance of the app gets low, sellers of the token are quickly disencentivized due to an exponentially decreasing exchange rate. Conversely, buyers are highly incentivized at this point. This makes it easy for the community to 'prop up' the value of their token with reserves of Bitcoin Cash, stabilizing the price in the event of market panics.
The major features of the curve are determined by the initial values of BCH and tokens. The examples in this post use the initial values of 25 BCH and 5000 tokens. This is not the initial state of the app, they are simply constants that determine important features like the pseudo-stable range of token balances and the point where the equation crosses the y-axis.
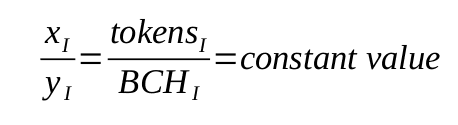
The initial values do create a constant (unchanging) value relationship between the token and the underlying asset (Bitcoin Cash). In the example above, 5000 tokens / 25 BCH creates a relationship of 200 tokens per BCH. This is the point where the equation crosses the y-axis.
When the token is near its psudo-stable point, 200 tokens will be exchangeable for 1 BCH. While the fiat value of BCH is free to change, this relationship between tokens and BCH will remain constant. It provides a basis upon which workers can value their time (in terms of tokens) relative to their market price in their local fiat economy.
Implementation
Implementing this basic math into an automatic market-making app consists of the following steps:
- Calculate the state of the app, based on its current BCH or token balance.
- Calculate the state of the app based on the new input from the user (BCH or tokens).
- Calculate the difference between the two states. Distribute the difference to the user.
Step 1: Calculating state based on BCH
The basic equation is helpful for conceptualization, and comparing to the Bancor whitepaper. But the axis needs to be swapped, since BCH is the finite resource, whereas tokens can be created and destroyed at-will by the governance of the community.
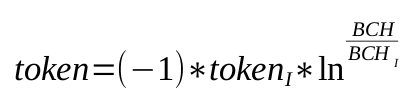

Step 2a: BCH In
If the user sent in BCH, this step calculates the new balances and determines how many tokens to send back in exchange for the BCH.
- Initial balances are known:
bch1 - The initial token balance can be calculated from bch1:
token1 - Input BCH is known:
bchIn - Solve for token output:
tokenOut

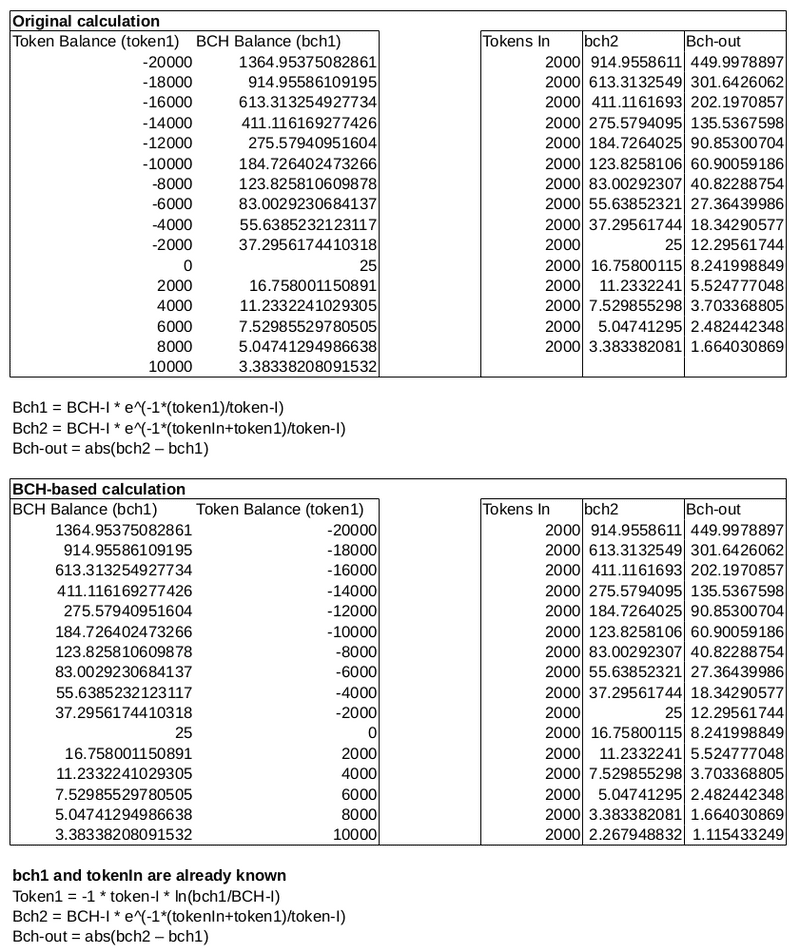
Step 2b: Tokens In
If the user sent in tokens, this step calculates the new balances and determines how much BCH to send to the the user. The math takes a little twist here. The 'original calculation' would determine the BCH to send based on the token balance. However, to combat transaction noise and knowing that BCH is the real finite resource, the 'BCH-based calculation' achieves the same result, and the implementation is based on the actual (rather than calculated) BCH balance of the app.
- Initial balances are known:
bch1 - The initial token balance can be calculated from bch1:
token1 - Input tokens are known:
tokenIn - Solve for token output:
bchOut
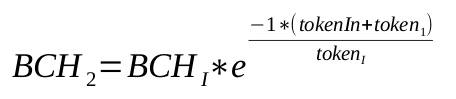
Step 3: Send difference to user
Once the two states have been calculated, the difference between the states can be sent to the user. Because the mathematics are rooted in the Bitcoin Cash balance of the app, it's incredibly important that the app be able to trust the data it's receiving about its BCH balance. For this reason, the app does not interact with zero-confirmation transactions, and only sends the output to the user after two block confirmations. This trade-off in slower performance essentially eliminates the risk of a double-spend or block-reorg attacks.
The mathematics described in this post are captured in two functions within the token-liquidity apps code base:
- exchangeBCHForTokens() handles step 2a for sending tokens to the user in exchange for BCH.
- exchangeTokensForBCH() handles step 2b for sending BCH to the user in exchange for tokens.
Burning Tokens
While the primary function of the token-liquidity app is to act as an automated market-maker, it has a very important secondary function: burning tokens.
For the Permissionless Software Foundation, the purpose of the token is to reward and acknowledge developers for their efforts, by reimbursing them with tokens. However, on the end-user side, tokens often create additional friction, which is highly undesirable.
The functionality of the token-liquidity app has been expanded to read and analyze OP_RETURN messages in BCH transactions. It's important to point out the functionality described in this section only applies to BCH transactions, where the user sends BCH to the token-liquidity app. It does not apply to transactions where users send tokens to the token-liquidity app. The SLP token protocol uses the OP_RETURN message in a different way.
When the token-liquidity app receives Bitcoin Cash, it will analyze the transaction to see if one of the outputs contains an OP_RETURN message. If that message contains the code 'BURN', then the app will burn the equivalent amount of tokens, instead of the default behavior of sending the tokens on to the user.
When the tokens are burned, they have the exact same effect on price, except the tokens are taken out of circulation, thereby passing that value on to the other tokens in circulation. i.e. The tokens held by the developers become more valuable.
This burning mechanism achieves two goals:
- End-users only need to deal with BCH and not tokens, thereby reducing friction. The sending of BCH to the token-liquidity app will be handled 'under the hood' and the end user does not even need to be aware of the token-economic model.
- By burning tokens and taking them out of circulation, it causes the price of token to rise. This effectively passes value backwards in the supply chain. Developers who have already been compensated in tokens, who have been holding them and waiting for the price to increase, can send them to the token-liquidity app and 'cash out' into BCH, and then into their local fiat.